Чем бозоны отличаются от фермионов?
Бозо́н (от фамилии физика Бозе) — частица с целым значением спина. Бозоны, в отличие от фермионов, подчиняются статистике Бозе — Эйнштейна, которая допускает, чтобы в одном квантовом состоянии могло находиться неограниченное количество одинаковых частиц.
Что такое функция распределения частиц по энергетическим состояниям?
Основная задача статистики состоит в определении числа частиц, энергия которых лежит в заданном интервале. Результатом решения этой статистической задачи является нахождение функции распределения частиц по энергиям, которую обозначают обычно f(E). Если dZ - число возможных состояний ансамбля частиц с энергией, заключенной в интервале от E до E+dE, а dN - число частиц, находящихся в этих состояниях, то по определению f(E)=dN/dZ
Для молекул идеального газа f(E) известна как функция распределения Максвелла-Больцмана
1. Что такое плотность электронных состояний?
функция распределения частиц по энергиям есть плотность заполнения данных состояний частицами.
2. Что такое функция распределения Бозе–Эйнштейна?
БОЗЕ-ЭЙНШТЕЙНА РАСПРЕДЕЛЕНИЕ - функция распределения по уровням энергии тождеств. частиц с нулевым или целочисл. спином при условии, что взаимодействие частиц слабое и им можно пренебречь, т. е. ф-ция распределения идеального квантового газа, подчиняющегося Бозе - Эйнштейна статистике.
В случае статистич. равновесия ср. число ni таких частиц в состоянии с энергией ei при темп-ре T выше вырождения температуры определяется Б--Э. р. 
Где i - набор квантовых чисел, характеризующих состояние частицы, µ - хим. потенциал.
Б.- Э. р. соответствует максимуму статистического веса (или энтропии) с учётом неразличимости частиц, отвечающей требованиям бозе-статистики. При темп-ре ниже темп-ры вырождения бозе-газ испытывает Бозе - Эйнштейна конденсацию, при к-рой часть частиц Скапливается в состоянии с нулевым импульсом, а остальные частицы распределены согласно Б.- Э. р. С µ=0
3. Что такое функция распределения Ферми–Дирака?
(ферми-распре-деление) - ф-ция распределения по уровням энергии тождественных частиц с полуцелым спином при условии, что взаимодействием частиц между собой можно пренебречь. Ф.- Д. р.- ф-ция распределения идеального квантового газа ( ферми-газа), подчиняющегося Ферми-Дирака статистике. Ф.- Д. р. соответствует максимуму статистического веса (или энтропии) с учётом неразличимости тождественных частиц (см. Тождественности принцип )и требований статистики Ферми - Дирака.
В системах частиц, описываемых антисимметричными волновыми функциями, осуществляется статистика Ферм-Дирака (распределение Ферми-Дирака), которая описывает поведение систем фермионов (электронов, протонов, нейтронов и др.) — частиц, подчиняющихся принципу запрета Паули и имеющих полу целый спин. В таких системах в одном квантовом состоянии может находиться не более одной частицы. Решение задачи о наиболее вероятном распределении частиц по состояниям, при условии сохранения полной энергии системы и полного числа ее частиц, приводит к распределению Ферми — Дирака:

4. Чем вырожденный идеальный газ бозонов отличается от невырожденного идеального газа?
Вырожденный газ, газ, свойства которого существенно отличаются от свойств классического идеального газа вследствие квантовомеханического влияния одинаковых частиц друг на друга. Это взаимное влияние частиц обусловлено не силовыми взаимодействиями, отсутствующими у идеального газа, а тождественностью (неразличимостью) одинаковых частиц в квантовой механике (см. Тождественности принцип). В результате такого влияния заполнение частицами возможных уровней энергии даже в идеальном газе зависит от наличия на данном уровне других частиц. Поэтому теплоёмкость и давление такого газа иначе зависят от температуры, чем у идеального классического газа; по-другому выражается энтропия, свободная энергия и т. д.
Вырождение газа наступает при понижении его температуры до некоторого значения, называемого температурой вырождения. Полное вырождение соответствует абсолютному нулю температуры.
При вырождении газа бозонов из частиц с отличной от нуля массой (такими бозонами могут быть атомы и молекулы) некоторая доля частиц системы должна переходить в состояние с нулевым импульсом; это явление называется Бозе — Эйнштейна конденсацией. Чем ближе температура к абсолютному нулю, тем больше частиц должно оказаться в этом состоянии. Однако, как уже говорилось, системы таких частиц при понижении температуры до очень низких значений переходят в твёрдое или жидкое (для гелия) состояния, в которых значительны силовые взаимодействия между частицами и к которым поэтому неприменимо приближение идеального газа. Явление Бозе — Эйнштейна конденсации в жидком гелии, который можно рассматривать как неидеальный газ из так называемых квазичастиц, приводит к появлению сверхтекучести.
http://ru.wikipedia.org/wiki/%C2%FB%F0%EE%E6%E4%E5%ED%ED%FB%E9_%E3%E0%E7
5. Чем идеальный вырожденный газ фермионов отличается от невырожденного идеального газа?
http://ru.wikipedia.org/wiki/%C2%FB%F0%EE%E6%E4%E5%ED%ED%FB%E9_%E3%E0%E7
6. Какие существуют основные типы кристаллов?
По типу связей различают пять классов кристаллов.
1. Кристаллы молекулярные (с Ван-дер-Ваальсовыми связями). Энергия связи в таких кристаллах имеет значения порядка величины 103 ÷104 Дж/моль. Примерами таких кристаллов являются кристаллы затвердевших инертных газов- неона, аргона, криптона, ксенона.
2. Кристаллы с ковалентной связью. Взаимодействие между частицами в таких кристаллах обусловлено тем, что два электрона принадлежат одновременно двум атомам. Энергия связи в таких кристаллах имеет значения порядка величины 105 ÷106 Дж/моль. Примерами таких кристаллов являются кристаллы кремния, алмаза.
3. Кристаллы с водородной связью. Эта связь обусловлена наличием водорода в веществах. Она слабее ковалентной. Энергия связи в таких кристаллах имеет значения порядка величины 104 Дж/моль. Примерами таких кристаллов являются кристаллы льда, вещества КН2РО-сегнетоэлектрика, применяемого в устройствах обработки информации, фтороводорода НF , синильной кислоты НСN, фторида аммония NH4F и др.
4. Кристаллы с ионной связью. Эта связь обусловлена взаимодействием ионов. Энергия связи в таких кристаллах имеет значения порядка величины 105 ÷106 Дж/моль. Примерами таких кристаллов являются кристаллы поваренной соли NaCl, фторида лития LiF.
5. Кристаллы с металлической связью. В металлах все валентные электроны слабо связаны с остовами атомов (положительными ионами, находящимися в узлах кристаллической решётки) и обобществлены, так что нельзя определить какой валентный электрон к какому остову относится. Валентные электроны в металлах уподобляют идеальному электронному газу, заполняющему пространство между узлами кристаллической решётки, в которых находятся положительные ионы. Энергия связи в таких кристаллах имеет значения порядка величины 104 ÷105 Дж/моль. Примерами таких кристаллов являются кристаллы всех металлов.
В кристаллах также возможны смешанные связи.
7. Что происходит с энергетическими уровнями атомов (молекул) при объединении их в кристалл?
Итак, при объединении атомов происходит расщепление энергетических уровней в зоны. И не только для валентных электронов, но для всех более высокоэнергетических. Так как определяется размерами кристаллической решетки, ширина энергетической зоны не зависит от размеров кристалла, а зависит от природы кристалла (рода атома, постоянной решетки).
Уровни электронов, лежащих в потенциальной яме, также расщепляются, т.к. не исключена возможность тунелирования и волновые функции этих электронов распространяются в других атомах. Чем ближе к ядру, тем меньше расщепление и их можно считать вырожденными
8. Как преобразуются одноэлектронные волновые функции при объединении атомов в кристалл?
9. Что такое энергетические зоны? Как они возникают?
Энергетические зоны - совокупность возможных значений энергии валентных электронов в кристаллах.
Энергетические зоны:
- состоят из большого, но конечного числа очень близких уровней энергии; и
- разделены интервалами запрещенных значений энергии электронов (запрещенными зонами).
Возникновение зон можно объяснить, рассматривая либо движение частицы в периодич. поле (приближение слабой связи), либо модификацию энергетич. уровней атомов при их сближении (приближение сильной связи, см. Зонная теория ).Простейший вариант объяснения состоит в том, что при сближении N одинаковых атомов происходит расщепление каждого уровня на N подуровней вследствие перекрытия электронных оболочек атомов. Если число N очень велико (N), то расстояния между подуровнями стремятся к 0. Это и означает возникновение Э. з. При введении в кристалл примесных атомов (концентрация к-рых такова, что возможно перекрытие их электронных оболочек) могут возникать новые Э. з. (примесные зоны).
10. Чем различается заполнение энергетических зон электронами в проводниках, полупроводниках и изоляторах?
http://allphysics.ru/kurs-fiziki/dielektriki-poluprovodniki-i-provodniki
11. Что такое работа выхода для данного вещества? Покажите ее на энергетической схеме?
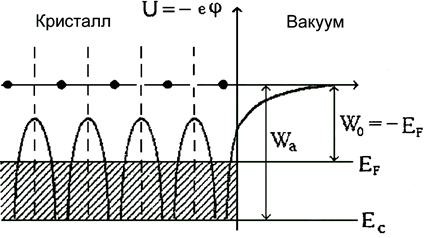
Работа выхода, энергия, затрачиваемая на удаление электрона из твёрдого тела или жидкости в вакуум. Переход электрона из вакуума в конденсированную среду сопровождается выделением энергии, равной Р. в.Рис. 1. Форма кристаллического потенциала U вдоль линии расположения ионов в кристалле и в приповерхностной области кристалла: положения ионов отмечены точками на горизонтальной линии; φ=-U/е – потенциал работы выхода; ЕF – энергия Ферми (отрицательная); ЕC – энергия дна зоны проводимости; WO – термодинамическая работа выхода; Wa – внешняя работа выхода; заштрихованная область условно изображает заполненные электронные состояния
12. Как распределены электроны по энергиям в зоне проводимости металла?
Распределение электронов по уровням валентной зоны и зоны проводимости описывается функцией Ферми-Дирака <ni>=1/[exp{(Ei-EF)/kT}+1].
13. Что такое уровень Ферми?
Уровень Ферми или электрохимический потенциал - это энергетический уровень, вероятность нахождения на котором для электрона равна 0.5 при любой температуре вещества. Численно уровень Ферми равен максимальной энергии электронов при температуре абсолютного нуля T = OK.
14. Как вычислить уровень Ферми для данного вещества?
ΔEg/2-0.75kT*ln(m*p/m*n)
15. Каким свойствами обладает уровень Ферми в металлах при низкой температуре? Как он зависит от температуры и от концентрации свободных электронов?
В полупроводниках при очень низких температурах уровень Ферми лежит посередине между дном зоны проводимости и потолком валентной зоны.
ΔEg/2-0.75kT*ln(m*p/m*n)
16. Где находится и как зависит от температуры уровень Ферми в чистых полупроводниках?
Уровень Ферми для чистых полупроводников лежит посередине запрещенной зоны EF=ΔE/2.
в чистом полупроводнике концентрации носителей зарядов зависят от ширины запрещенной зоны и при увеличении температуры возрастают приблизительно по экспоненциальному закону (температурные изменения А играют незначительную роль). Равенство концентраций ni и pi показывает, что такой полупроводник обладает одинаковыми электронной и дырочной электропроводностями и называется полупроводником с собственной электропроводностью.
17. Где находится и как зависит от температуры уровень Ферми в примесных полупроводниках?
Наличие примесных уровней в полупроводниках существенно изменяет положение уровня Ферми ЕF. Расчеты показывают, что в случае полупроводников n-типа уровень Ферми ЕF0 при 0 К расположен посередине между дном зоны проводимости и донорным уровнем (рис. 321), С повышением температуры все большее число электронов переходит из донорных состояний в зону проводимости, но, помимо этого, возрастает и число тепловых флуктуаций, способных возбуждать электроны из валентной зоны и перебрасывать их через запрещенную зону энергий. Поэтому при высоких температурах уровень Ферми имеет тенденцию смещаться вниз (сплошная кривая) к своему предельному положению в центре запрещенной зоны, характерному для собственного полупроводника.
Уровень Ферми в полупроводниках р-типа при 0 К ЕF0 располагается посередине между потолком валентной зоны и акцепторным уровнем (рис. 322). Сплошная кривая опять-таки показывает его смещение с температурой. При температурах, при которых примесные атомы оказываются полностью истощенными и увеличение концентрации носителей происходит за счет возбуждения собственных носителей, уровень Ферми располагается посередине запрещенной зоны, как в собственном полупроводнике.
18. Как выглядят одноэлектронные волновые функции в идеальном кристалле (функции Блоха)?
http://nuclphys.sinp.msu.ru/solidst/physmet2.htm
19. Что такое квазиимпульс электрона в кристалле?
Особенности движения электронов в кристалле обусловлены их взаимодействием с кристаллической решеткой. Оказывается, что движение отдельного электрона в кристалле можно описывать тем же уравнением, что и для свободной частицы, т.е. в виде второго закона Ньютона, в котором учитываются только внешние по отношению к кристаллу силы.
Рассмотрим движение электрона в кристалле под действием внешнего электрического поля. Внешнее электрическое поле приводит к увеличению скорости электрона и, следовательно, его энергии. Поскольку электрон в кристалле - это микрочастица, описываемая волновой функцией, то энергия электрона зависит от его волнового вектора. Зависимость между этими двумя характеристиками электрона в кристалле определяется дисперсионным соотношением, которое в свою очередь зависит от строения энергетических зон. Поэтому при расчете движения электрона в кристалле необходимо исходить из закона дисперсии.
Свободный электрон описывается монохроматической волной де Бройля и электрон в этом состоянии нигде не локализован. В кристалле же электрону необходимо сопоставить группу волн де Бройля с различными значениями частот w и волновых векторов k. Центр такой группы волн перемещается в пространстве с групповой скоростью
Эта групповая скорость соответствует скорости перемещения электрона в кристалле.
Задачу о движении электрона будем решать для одномерного случая. Увеличение энергии электрона dE под действием внешней силы F равно элементарной работе dA, которую совершает внешняя сила за бесконечно малый промежуток времени dt: Учитывая, что для электрона как микрочастицы
Учитывая, что для электрона как микрочастицы  имеем следующее выражение для групповой скорости
имеем следующее выражение для групповой скорости Подставляя полученное выражение для групповой скорости в формулу (2.16), получим
Подставляя полученное выражение для групповой скорости в формулу (2.16), получим отсюда
отсюда 
Распространяя этот результат на трехмерный случай, получим векторное равенство  Как видно из этого равенства, величина ћkдля электрона в кристалле изменяется со временем под действием внешней силы точно так же, как импульс частицы в классической механике
Как видно из этого равенства, величина ћkдля электрона в кристалле изменяется со временем под действием внешней силы точно так же, как импульс частицы в классической механике  Несмотря на это, ћkнельзя отождествить с импульсом электрона в кристалле, поскольку компоненты вектора k определены с точностью до постоянных слагаемых вида
Несмотря на это, ћkнельзя отождествить с импульсом электрона в кристалле, поскольку компоненты вектора k определены с точностью до постоянных слагаемых вида 
(здесь a - параметр кристаллической решетки, ni=1, 2, 3, ...). Однако в пределах первой зоны Бриллюэна ћkобладает всемисвойствами импульса. По этой причине величину ћk называют квазиимпульсом электрона в кристалле.
20. Как зависимость энергия электронов в кристалле от квазиимпульса (дисперсионная кривая)?
Закон дисперсии для электрона в кристалле

21. Что такое зоны Бриллюэна? Где они находятся? Как связаны с «длинами волн» одноэлектронных волновых функций?
многогранники, построенные по определенным правилам в обратной решётке кристалла. Первая зона Бриллюэна содержит все физически неэквивалентные наименьшие разрешённые квазиимпульсы, характеризующие состояние электронов. Форма зон Бриллюэна определяется симметрией кристалла. Понятие зоны Бриллюэна используется в теории твёрдого тела.
22. Что такое эффективная масса электрона в кристалл?

Величину m* называют эффективной массой электрона в кристалле.
Строго говоря, эффективная масса электрона никакого отношения к массе свободного электрона не имеет. Она является характеристикой системы электронов в кристалле в целом. Вводя понятие эффективной массы, мы реальному электрону в кристалле, связанному взаимодействиями с кристаллической решеткой и другими электронами, сопоставили некую новую свободную “микрочастицу”, обладающую лишь двумя физическими параметрами реального электрона - его зарядом и спином. Все остальные параметры - квазиимпульс, эффективная масса, кинетическая энергия и т.д. - определяются свойствами кристаллической решетки. Такую частицу часто называют квазиэлектроном, электроном-квазичастицей, носителем отрицательного заряда или носителем заряда n-типа, чтобы подчеркнуть ее отличие от реального электрона.
23. Почему эффективная масса электрона в кристалле, вообще говоря тензор?
Те́нзор эффекти́вной ма́ссы — термин физики твёрдого тела, характеризующий сложную природу эффективной массы квазичастицы (электрона, дырки) в твёрдом теле. Тензорная природа эффективной массы иллюстрирует тот факт, что в кристаллической решётке электрон движется не как частица с массой покоя, а как квазичастица, у которой масса зависит от направления движения относительно кристаллографических осей кристалла. Эффективная масса вводится, когда имеется параболический закон дисперсии, иначе масса начинает зависеть от энергии. В связи с этим возможна отрицательная эффективная масса.
24. Выпишите основные уравнения динамики электронов в кристаллической решетке?
http://phys.bspu.unibel.by/static/lib/phys/bmstu/tom6/ch4/texthtml/ch4_1.htm
поиск по «динамика электронов»
25. Что такое дырки? Каковы их заряд и масса?
Таким образом, последовательное перемещение электронов по энергетическим уровням под влиянием электрического поля эквивалентно перемещению вакантного состояния. Квантовое состояние, не занятое электроном в энергетической зоне, называется дыркой.
Во время разрыва связи между электроном и ядром появляется свободное место в электронной оболочке атома. Это обуславливает переход электрона с другого атома на атом со свободным местом. На атом, откуда перешёл электрон, входит другой электрон из другого атома и т. д. Это обуславливается ковалентными связями атомов. Таким образом, происходит перемещение положительного заряда без перемещения самого атома. Этот условный положительный заряд называют дыркой.
26. Как связана электропроводность кристалла со структурой заполнения энергетических зон?
Структура энергетических зон кристалла оказывает решающее влияние на величину его электропроводности. Поскольку электрический ток есть направленное движение зарядов (в металлах - электронов), то возникновение электрического тока связано с увеличением импульса электронов вдоль направления действующей на него силы. Вместе с импульсом электрона меняется его волновой вектор. Поскольку энергия и волновой вектор электрона - две взаимосвязанные величины, связь между которыми определяется дисперсионным соотношением, то увеличение волнового числа должно обязательно сопровождаться увеличением энергии электрона. Нетрудно оценить, каково увеличение энергии электрона за счет его ускорения в электрическом поле, вызывающим электрический ток в проводниках. Если величина напряженности электрического поля равна 104 В/м, то на расстоянии, равном средней длине свободного пробега электрона в кристалле, а она обычно составляет ~10-8 м, электрон приобретает энергию приблизительно 10-4 эВ. Понятно, что эти значения энергии позволяют электрону переходить с уровня на уровень только внутри одной энергетической зоны. Для перехода между зонами необходима энергия больше ширины запрещенной зоны Eg, которая, как указывалось выше, составляет 0.1 ... 10 эВ.
27. Как и почему зависит концентрация свободных носителей в проводнике и полупроводнике от температуры?
концентрация носителей заряда в собственном полупpоводнике определяется шириной запрещенной зоны и температурой. С ростом температуры она растет по экспоненциальному закону.
n=A . EXP(-Wo/2kT),
28. Чем определяется концентрация свободных электронов и “дырок” в полупроводниковом кристалле?
Для собственного полупроводника концентрация свободных носителей заряда в зависимости от температуры определяется выражением
n=A . EXP(-Wo/2kT),
где
n - концентрация носителей заряда;
Wo - ширина запрещенной зоны;
k постоянная Больцмана;
A константа, зависящая оттемпературы;
29. Что такое донорная и акцепторная примесь? Как они влияют на энергетический спектр электронов в полупроводнике?
Донорные примеси - атомы химических элементов, внедренные в кристаллическую решетку полупроводника и создающие дополнительную концентрацию электронов. Донорными примесями являются химические элементы, внедренные в полупроводник с меньшей, чем у примеси, валентностью.
Акцепторные примеси - атомы химических элементов, внедренные в кристаллическую решетку полупроводника и создающие дополнительную концентрацию дырок.Акцепторными примесями являются химические элементы, внедренные в полупроводник с большей, чем у примеси, валентностью.
Аналогичным образом примеси, акцепторы или доноры, создают акцепторные или донорные уровни, лежащие в запрещённой зоне. Они значительно модифицируют спектр поглощения легированного полупроводника.
30. Как и почему зависит подвижность свободных носителей в проводнике и полупроводнике от температуры.
Подвижность носителей заряда определяется по этой теории следующим образом:
Μ=e*<λ>/m*e/<V>
, (5)
где <λ> – средняя длина свободного пробега электрона;
m*e– эффективная масса электрона в металле;
<V>– средняя общая скорость движения электронов
31. Как зависит электропроводность металлов от температуры?
влено в ряде случаев, что эта зависимость близка к линейной зависимости. Обычно ее приводят в виде температурной зависимости удельного сопротивления.
r(T)= r(T0)(1+ TКr(T-T0))
Здесь r( T0) - удельное сопротивление при какой—то температуре T0, обычно это 20°С. TКr - температурный коэффициент удельного сопротивления. Он имеет размерность 1/К (или 1/°С), для металлов TКr всегда положителен.
32. Как зависит электропроводность чистых полупроводников от температуры?
Электропроводимость химически чистого полупроводника возможна в том случае, когда ковалентные связи в кристаллах разрываются и появляются свободные электроны. Например, нагревание даже до небольших температур приводит к разрыву ковалентных связей, появлению свободных электронов и возникновению собственной электронной проводимости чистого полупроводника (проводимости n-типа). После ухода электрона со своего места в этой области кристалла нарушилась его нейтральность. В том месте, откуда ушел электрон, возникает избыточный положительный заряд — образуется положительная "дырка" (рис. 1). Она обладает положительным зарядом, равным по модулю заряду электрона. На освободившееся от электрона вакантное место — дырку — может перескочить другой электрон, а это эквивалентно перемещению дырки в направлении, противоположном направлению движения электрона. В отсутствие внешнего электрического поля эти свободные электроны и дырки движутся в кристалле полупроводника хаотически. С повышением температуры возрастает число разрывов ковалентных связей и увеличивается количество свободных электронов и дырок в кристаллах чистых полупроводников, а следовательно, возрастает удельная электропроводность и уменьшается удельное сопротивление чистых полупроводников.
33. Как зависит электропроводность примесных полупроводников от температуры?
В примесном полупроводнике n ¹ p, поэтому электропроводность выражается следующей формулой:
σ = е (μnn + μpp)
При повышении температуры энергия электронов, а следовательно, и подвижность увеличивается. Но, начиная с некоторой температуры Т усиливаются колебания узлов кристаллической решетки полупроводника, которые мешают перемещению свободных носителей зарядов. Следовательно, их подвижность падает
34. Что такое внутренний фотоэффект?
Внутренним фотоэффектом называется перераспределение электронов по энергетическим состояниям в твердых и жидких полупроводниках и диэлектриках, происходящее под действием излучений. Он проявляется в изменении концентрации носителей зарядов в среде и приводит к возникновению фотопроводимости или вентильного фотоэффекта.
Фотопроводимостью называется увеличение электрической проводимости вещества под действием излучения.
35. Сформулируйте закон Дюлонга-Пти.
молярная теплоёмкость твёрдых тел при комнатной температуре близка к 3R
36. Что такое фононы? Как определяется их энергии и квазиимпульс?
Фоно́н — квазичастица. Фонон представляет собой квант колебательного движения атомов кристалла.
Энергия фононовФононы обладают линейным законом дисперсии. Энергия фононов связана с квазиимпульсом следующим простым выражением:
E=cp, где с ≈ 240 м/с — скорость звука в гелии.
37. Почему при низкой температуре зависимость теплоемкости от температуры отклоняется от закона Дюлонга-Пти?
Позднее было обнаружено отклонение от закона Дюлонга и Пти для всех веществ при низких температурах, близких к абсолютному нулю. Причём, теплоёмкость стремится к нулю при стремлении температуры к абсолютному нулю. Таким образом, была обнаружена зависимость теплоёмкости твёрдых тел от температуры в области низких температур, причём теплоёмкость убывала по закону:С~1/Т 3 . Попытки объяснить температурную зависимость (рис.7.1) теплоёмкости твёрдых тел были сделаны Эйнштейном. Однако правильное объяснение такой зависимости было дано Дебаем на основе квантовых законов.
http://ru.wikipedia.org/wiki/Модель_Дебая
38. Почему электроны проводимости вносят очень малый вклад в теплоемкость металлического кристалла (по сравнению с колебаниями решеткой)?
Электроны проводимости вносят низкий вклад в теплоемкость металла (закон Дюлонга-Пти). Теоретический же расчет по модели Друде показывает,что вклад электронов в теплоемкость должен быть значительным. Предположительно, в реальном пространстве, зона проводимости должна находится в районе поверхности ячейки Вигнера-Зейтца. Грубо, она напоминает собой пчелиные соты. Поэтому электроны проводимости вносят низкий вклад в теплоемкость металла, т.к. они по сути находятся в пространстве двумерном со сложной поверхностью. Здесь ошибка Друде. А периодичность для электрона проводимости в кристалле связана не столько с постоянной решетки, сколько со стереометрией гибридных (валентных) орбиталей атомных остовов. Смотри осциляции в опытах де-Гааза-ван-Альфена по исследованию поверхности Ферми.
· Эффект Джозефсона ? Появилось много сообщений о сопутствующих сверхпроводимости магнитных явлениях. Поэтому представляется интересным расположить между двумя сверхпроводниками тонкий слой из ферромагнетика (железа например) или из диамагнетика-меди и проанализировать результат. Не сделает ли какой-нибудь из этих сэндвичей более высокой Тс?
· Повышение Тс. Согласно выше изложенного. Для повышения Тс в металлах могу предложить следующее. Отрицательно зарядить металлический образец и испытать его.
39. Почему металлический кристалл имеет относительно большую теплопроводность?
Высокая теплопроводность металлов тоже объясняется наличием свободных электронов в межатомном пространстве - они легко "откликаются" на изменения энергии и способствуют ее быстрому переносу в кристалле.
40. Сформулируйте основные положения теории Дебая теплоемкости кристаллической решетки?
каждый ион действием своего электрического заряда поляризует окружение и образует вокруг себя некоторое преобладание ионов противоположного знака — так называемую ионную атмосферу.
В отсутствие внешнего электрического поля ионная атмосфера имеет сферическую симметрию, и её заряд равен по величине и противоположен по знаку заряду создающего её центрального иона. В этой теории не уделено почти никакого внимания образованию пар противоположно заряженных ионов путём непосредственного взаимодействия между ними
41. Как в теории Дебая вычисляется внутренняя энергия колебаний кристаллической решетки?
Внутренняя энергия пропорциональная четвертой степени температуры
U=aT^4
42. Что такое температура Дебая?
Дебая температура, физическая константа вещества, характеризующая многие свойства твёрдых тел — теплоёмкость, электропроводность, теплопроводность, уширение линий рентгеновских спектров, упругие свойства и т. п. Введена впервые П. Дебаем в его теории теплоёмкости. Д. т. определяется формулой:
QD = hvD /k,
где k — Больцмана постоянная, h — Планка постоянная, vD — максимальная частота колебаний атомов твёрдого тела. Д. т. приближённо указывает температурную границу, ниже которой начинают сказываться квантовые эффекты. При температурах Т>>QD теплоёмкость кристалла, состоящего из атомов одного сорта, при постоянном объёме CV = 6 кал (°С×моль)-1 в соответствии с законом Дюлонга и Пти. При T<<QD теплоёмкость пропорциональна (T/ QD)3 (закон T3 Дебая).
43. Учет ангармонизма колебаний атомов. Тепловое расширение.
http://nuclphys.sinp.msu.ru/solidst/physmet8.htm
44. Какие явления называются контактными?
КОНТАКТНЫЕ ЯВЛЕНИЯ В ПОЛУПРОВОДНИКАХ - неравновесные электронные явления, возникающие при прохождении электрич. тока через контакт полупроводника с металлом или электролитом или через контакт двух различных полупроводников (гетеропереход)либо через границу двух областей одного и того же полупроводника с разным типом носителей заряда (см. р - п-переход)и разной их концентрацией.
Приведение в контакт дву